-update:
출처와 이름을 밝히더라도 팀원 분들께서 참여하신 부분에 대한 내용은 이 블로그에 포스팅하는 것은 적절하지 않을 것이라는 뒤늦은 판단으로 관련 내용은 모두 삭제하였습니다.
문제 1. 해당 강의에서는 "시그모이드(sigmoid) 함수나 tanh함수는 전통적으로 많이 쓰이던 활성함수지만 딥러닝에선 ReLU함수를 많이 쓰고 있다." 라고 말하고 있다. 활성화 함수의 개념에 대해 다시 한번 찾아보고, 각 함수마다의 특징들을 찾아보고 어느 모델, 기능들에 사용이 되는지, 또 왜 딥러닝에서는 ReLU 함수를 많이 사용하고 있는지에 대해 토의해보자 . [ 주제 : 신경망(활성화 함수) ]
(중략..)
활성 함수들 python으로 구현해보기
활성화 기능은 신경망의 중요한 구성 요소입니다. 이는 네트워크의 다른 계층에서 수신된 입력 신호에 수학적 변환을 적용하여 신경망의 출력을 결정하는 데 도움이 됩니다. 활성화 기능을 사용하면 입력 데이터 포인트와 출력 데이터 포인트 간의 복잡한 비선형 관계를 허용할 수 있습니다. 어떤 기능이 적절한지 선택하는 것은 모델을 사용하여 해결하려는 문제와 하드웨어 기능 또는 시간/공간 제한으로 인한 제약에 따라 크게 달라집니다.
신경망 활성화 함수 는 모델에 비선형성을 도입하는 함수입니다. 신경망은 각 계층에 여러 개의 노드를 갖고 있으며, 완전 연결 네트워크에서는 한 계층의 모든 노드가 다음 계층의 모든 노드에 연결됩니다. 예컨데, 두 번째 레이어의 첫 번째 뉴런 값을 계산하는 방법을 살펴보면, 첫 번째 레이어의 각 뉴런에 가중치를 곱하고(가중치는 훈련을 통해 학습함), 곱해진 값을 더하고, 그 합을 편향에 더합니다. 이 과정에서 편향도 학습하게 됩니다.
비유
신경망이 호스라고 상상해 보면, 물을 취하고(일부 입력을 받음), 물을 어딘가로 운반하고(입력을 수정하고), 물을 밖으로 밀어냅니다(일부 출력을 생성함). 활성화 기능이 없으면 호스는 강철 파이프처럼 고정되고 유연하지 않게 작동합니다. 때로는 그것만으로도 충분합니다. 물을 공급하기 위해 파이프를 사용하는 데에는 아무런 문제가 없습니다.
단단한 강철 파이프(신경망의 선형)는 아무리 회전해도 맞지 않습니다. 활성화 함수는 함수를 더욱 유연하게 만들어주기 때문에 편리합니다. 이 경우 활성화 기능이 있는 신경망은 플라스틱 정원 호스처럼 작동합니다. 특정 요구 사항에 맞게 구부릴 수 있으며 강철 파이프로는 도달할 수 없는 훨씬 더 많은 장소로 물을 운반할 수 있습니다.
따라서 활성화 함수의 목적은 호스에 유연성(신경망의 비선형성)을 추가하는 것입니다.
- 패키지 설치, x값 정의하기(그래프를 그리기위한 용도와 값을 구하기 위한 용도 두가지로 선언)
- sign
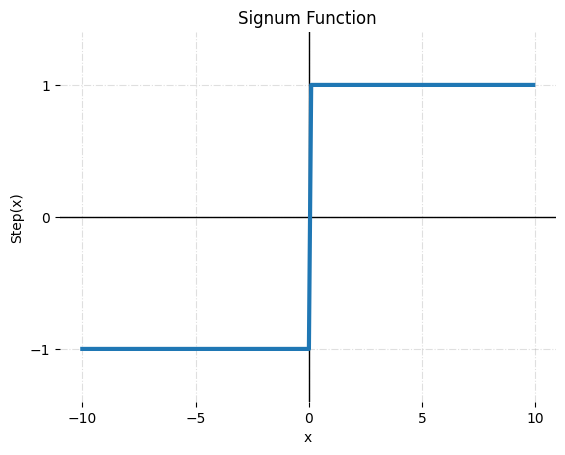
- Binary Step
계단 함수의 경우 0 또는 1이 출력
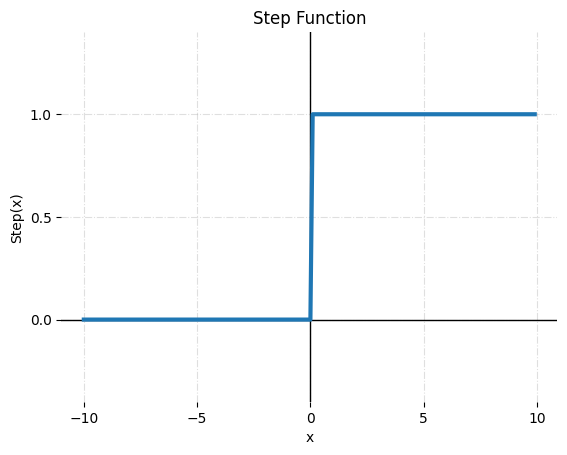
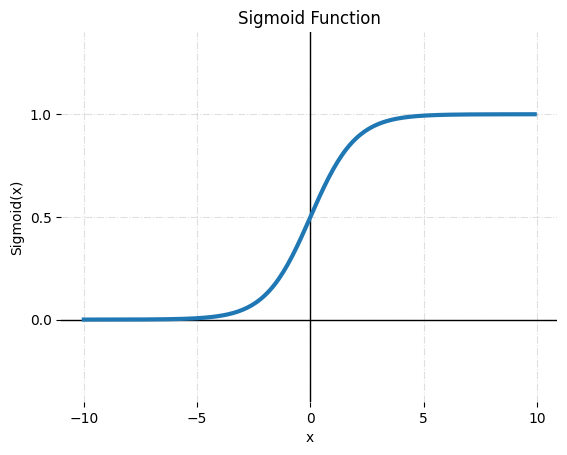
- sigmoid
시그모이드 함수는 이진 분류 문제에 널리 사용되는 도구로, 입력 값을 0과 1 사이의 값으로 매핑합니다. 이를 통해 출력을 양성 클래스의 확률을 나타내는 것으로 해석할 수 있습니다
- 인공 신경망에서 정보를 분류하는 데 사용되는 수학적 함수입니다.
- 모든 입력을 0과 1 사이의 값에 매핑한 다음 true 또는 false로 해석할 수 있습니다. 시그모이드 함수를 사용하면 0 ~ 1 사이의 연속적인 실수가 출력된다
- (사용 예) : 이미지 인식 시스템이 이미지의 개체가 고양이인지 아닌지를 결정해야 하는 경우입니다. 해당 특정 개체에 대한 시그모이드 활성화 함수의 출력이 0.5를 초과하면 "고양이와 유사한" 개체로 분류됩니다. 그렇지 않으면 그렇지 않습니다.
- (장점) : 다른 활성화 기능에 비해 이 활성화 기능을 사용하면 작은 변화가 결과에 너무 많은 영향을 미치지 않도록 데이터 포인트를 평활화하여 전체적으로 예측을 더욱 신뢰할 수 있다는 장점이 있습니다.
- (단점) : 이 함수는 "그라데이션 소멸" 문제가 있습니다.
- (참고) : 우리는 Sigmoid가 0과 1 사이의 값을 반환한다는 것을 알고 있습니다. 이는 특정 클래스에 속하는 데이터 포인트의 확률로 처리될 수 있습니다. 따라서 시그모이드는 "이진 분류" 문제에 자주 사용됩니다.
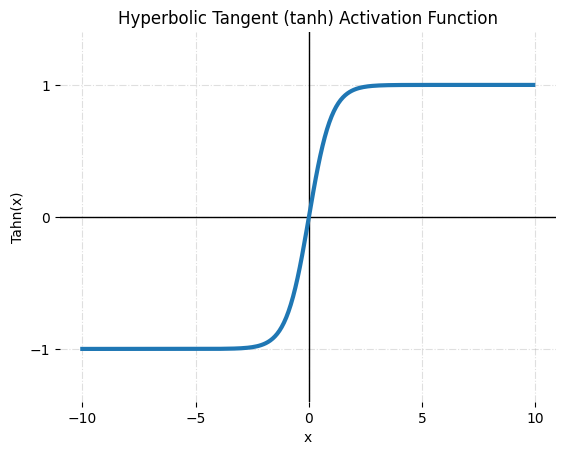
- tanh
tanh(하이퍼볼릭 탄젠트) 활성화 함수는 sigmoid 시그모이드와 유사하지만 sigmoid 시그모이드와 비교할 때 몇 가지 뚜렷한 차이점이 있습니다. Sigmoid처럼 0 또는 1이 아닌, -1과 1 사이의 값에 입력을 매핑하는 대신 개체를 범주 기반으로 분류할 때 더 많은 뉘앙스를 허용합니다.
- (장점) : 네트워크에서 한 번에 고려되는 모든 기능에 대한 유사성 점수(즉, 다차원 분류). Tanh은 또한 Sigmoid 함수보다 더 나은 그래디언트 속성을 가지고 있습니다. 즉, 각 축의 곡률 효과로 인해(Sigmoid에서 생성된 것과 같은 평평한 선과 반대) 그래디언트가 왜곡이 적은 레이어를 통해 다시 전파될 수 있기 때문에 훈련 중에 더 빠른 학습 속도를 허용한다는 의미입니다. 따라서 정확성이 가장 중요한 딥 러닝에 자주 사용될 수 있다
- (단점) : 이 함수는 그라데이션 소멸 문제가 있습니다.
- softmax
입력이 주어지면 가능한 모든 클래스에 대한 확률 분포를 반환합니다. 이는 여러 객체가 하나의 이미지에 동시에 나타날 수 있는 이미지 인식과 같은 다중 클래스 분류 작업에 유용할 수 있습니다.
- Softmax 함수는 종종 다중 시그모이드의 조합으로 작성됩니다.
- 우리는 Sigmoid가 0과 1 사이의 값을 반환한다는 것을 알고 있습니다. 이는 특정 클래스에 속하는 데이터 포인트의 확률로 처리될 수 있습니다. 따라서 시그모이드는 이진 분류 문제에 자주 사용됩니다.
- 소프트맥스 함수는 다중 클래스 분류 문제에 사용될 수 있습니다. 이 함수는 각 고유 클래스에 속하는 데이터 포인트의 확률을 반환합니다.
소프트맥스 함수는 분류 문제를 다룰 때 사용되는 활성화 함수입니다
- 입력받은 값들을 0 ~ 1 사이 값으로 정규화한다.
- 출력값들의 총합은 항상 1이 된다.
- 입력값 x가 n개 일 때 다음 수식으로 나타낼 수 있다.
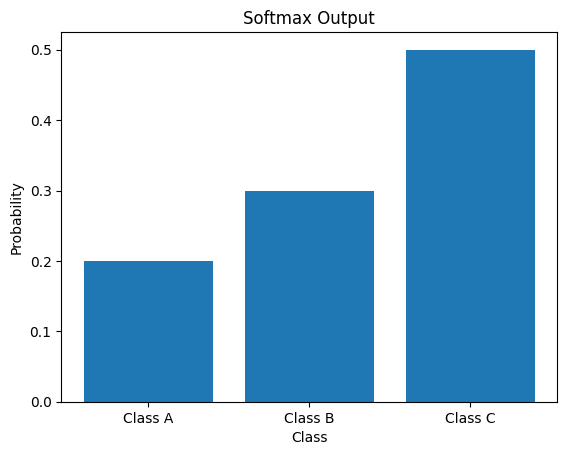
소프트맥스 함수는 여러 클래스에 대한 확률 분포를 출력하므로 분류 작업의 맥락에서 일반적으로 사용됩니다. 그러나 소프트맥스 함수 자체는 값 벡터를 입력으로 사용하고 확률 벡터를 반환하므로 그래프를 그리는 것은 의미가 없습니다.
특정 예에 대한 소프트맥스 함수의 출력을 시각화하려면 각 클래스에 할당된 확률을 나타내는 막대 차트를 그릴 수 있습니다. 다음은 소프트맥스 출력에 대한 막대 차트를 그리는 Python 코드 조각의 예입니다.
- ReLU
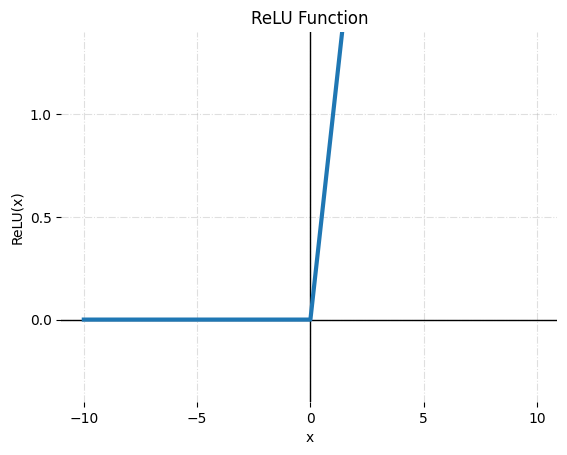
입력의 최대값을 반환하거나 음수인 경우 0을 반환합니다.
- rectified 는 '정류된'이라는 의미로, ReLU 함수는 음수를 0으로 만든다. 즉, 입력이 0 이하일 경우에는 0을 출력하지만 입력이 0을 넘으면 입력 받은 값을 그대로 출력한다.
- 참고: 히든 레이어의 경우 Relu를 사용하는 것이 가장 효과적인 옵션입니다. 계산적으로 매우 효과적입니다. 또한 값이 0보다 작은 것처럼 그래디언트 소실 문제가 발생합니다. 그러면 출력이 0이 된다는 것은 상수를 의미합니다.
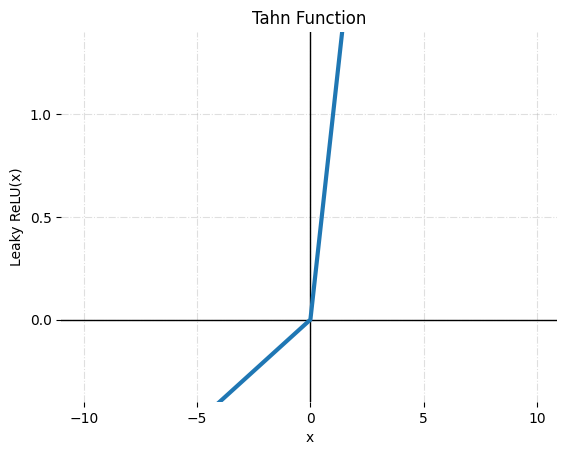
- Leaky ReluLeaky Relu는 ReLU의 변형입니다. Leaky ReLU라는 변형은 음수 값이 발견될 때 입력 또는 작은 양수 상수를 곱한 입력을 반환하여 뉴런이 항상 0을 출력하는 것을 방지합니다.
(z < 0)인 경우, ReLU는 0이 되는 대신, Leaky ReLU는 0이 아닌 작은 상수 기울기 α(일반적으로 α = 0.01)를 허용합니다.
2. 토의내용 + 결론
- (1) 일단, 주요 활성화 함수를 ‘한 눈에’ 볼 수 있는 그래프 그려보자
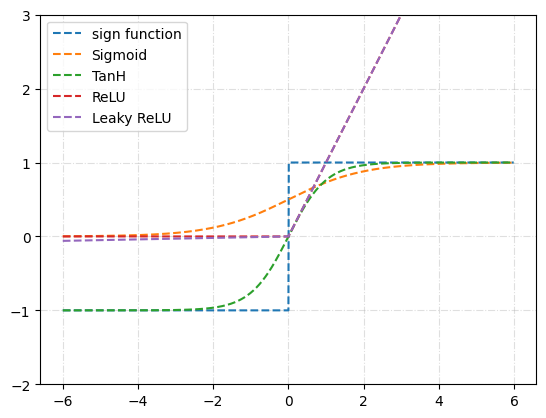
- (2) 검색을 해보니,, 렐루relu 활성 함수가 보편적으로 많이 사용한다고하지만.. 내(우리) 상황이 그들의 보편적 상황과 동일한지 여부는 다른 문제가 아닐까? 그렇다면 전문가?들이 각 상황 또는 절차별 활성함수를 선정하는 기준을 찾아보는 건 어떨까?
| 사용되는 층 | 용도 | 활성화 함수 |
| 은닉층 | 기울기 소실 문제를 줄이고 다음 층으로 신호 전달 |
렐루(ReLU) |
| 리키 렐루(Leaky ReLU) | ||
| 출력층 | 이진 분류 | 시그모이드(Sigmoid) |
| 다중 분류 | 소프트맥스(Softmax) | |
| 회귀 | 활성화 함수 사용 X |
**참고 레퍼런스
- https://happy-obok.tistory.com/55
- https://towardsdatascience.com/activation-functions-neural-networks-1cbd9f8d91d6
- https://www.shiksha.com/online-courses/articles/activation-functions-with-real-life-analogy-and-python-code/
- https://blog.naver.com/wideeyed/221017173808
- https://blog.naver.com/baek2sm/222010223220
'새로워지기 > 사이드 프로젝트' 카테고리의 다른 글
| LET’s AI 2024 코칭 스터디 - 4주차, 팀 미션 : nn.Pytorch tutorial (0) | 2024.06.17 |
|---|---|
| 어쩌다 휴먼 벡터 Human Vector (0) | 2024.06.15 |
| 데이터 분석 및 시각화 실습 - 기상 자료(서울 날씨) (0) | 2024.06.08 |
| LET’s AI 2024 코칭 스터디 - 1주차, 팀 미션 (0) | 2024.05.27 |
| 시각 지능 | 신호등 신호 분류기( feat. yolo v8, roboflow 데이터 증강) (0) | 2023.10.03 |




댓글